3、有限单元法
有限单元法是板结构进行数值计算常用的有效方法。将
平板弯曲问题简化为二维问题,且全部
应力和应变可以用板中面的挠度W表示,在平板弯曲问题的有限分析中,首先将结构
离散为单元,单元体的数目任意选择,例如x方向分成m等分,y方向分成n等分,单元数为m *n个;结点数目为(m+1) x (n+1)个。各个单元内的挠度W表示为通常的插值形式:

建立每个单元的
刚度矩阵K和执行标准化步骤,求解系统结点参数。的矩阵方程:
Ka=P
其中P为系统的载荷向量。
建立和上节偏微分方程及边界方程相等效的最小位能原理的泛函表达式∏p。现在统函∏p中出现的W的导数最高阶次是2,根据收敛准则,单元交界面上必须保持W及一阶导数的连续性,即挠度和
转角的连续性,要求插值函数具有C1连续性。
基于经典薄板理论的板单元,以W为场函数的板单元。由于本问题的总体域是矩形的,拟构造矩形单元的抽值函数,开始可以利用笛卡儿坐标的多项式:
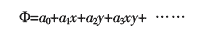
用以构造Lagramge矩形单元或Hermite矩形单元。
依据最小位能原理对泛函∏p变分,保证每个单元满足平衡条件,广义力满足连续条件。
对号入座,建立总体刚度矩阵和载荷矩阵。
协调单元和非协调单元边界条件的处理,保证计算过程的精确度和快速收敛性。
以上为薄板有限单元法的计算编制程序的准则,现已有通用程序可以借鉴,例如SAP90、SAP84、SAP93等,解决工程应用的问题。
4、幕墙计算结果
幕墙工程实例:
玻璃幕墙矩形a=870mm,L=1320mm,



点支玻璃幕墙具有视线通透,简洁明快,将建筑内外空间与装饰功能有机地融为一体,受到
建筑设计师的青、睐,发展迅速,玻璃幕墙的计算引起工程师们的广泛关注。本文采用
有限元法的计算,提出的简化模型及工程应用的方法具有重要的实用价值。
参考文献:
[1] 姜青海,刘祚秋,郭金基.高层
建筑玻璃幕墙简化模型的计算[J].湖南大学学报,2001,(4):109一112.
[2] 黄载生等编.
弹性力学与应用[M].杭州:浙江出版社,1989.
[3] 王冒成,邵敏编等.有限单元法基本原理和数值方法(第2
版)[M].北京:清华大学出版社,1987.
[4] 徐芝伦著.弹性力学[M].北京:高等教育出版社,1990.
与【】相关热点资讯:
【了解更多 “” 相关信息请访问
幕墙专区 】
 上一页12下一页
上一页12下一页
